위에서 아래로 일방향, 계층구조인 트리와 다르게
그래프는 어떤 노드들과도 연결될 수 있다.
마치 지하철 노선도 처럼

다양한 그래프 종류들!

그래프는
연결점(노드)과 연결점 사이를 잇는 간선으로 이루어져 있다.
그래프는 표현하는 방법은
크게 3가지가 있다.
1. 인접리스트 (adjacency list)
모든 노드에 연결된 노드들을 순서대로 기록한 리스트
연결된 노드만 기록한다.
파이썬에서 딕셔너리를 써서 키 : 값으로 적어서 사용 많이 함.

const graph = [[2,3],[1,3],[1,2,4],[3]]
2. 인접행렬 (adjacency matrix)
그래프에서 어느 연결점(노드)들이 변(간선)으로 연결되었는지 나타내는 정사각 행렬

가로 123456 세로 123456 노드
(가로,세로)
(1,1) 자기 자신은 연결할 수 없어서 0
(1,2) 연결되어서 1 임
무방향 그래프에서 인접행렬은 다음과 같이 대칭이다.
const graph = [
[0, 1, 0, 0, 1, 0],
[1, 0, 1, 0, 1, 0],
[0, 1, 0, 1, 1, 0],
[0, 0, 1, 0, 1, 1],
[1, 1, 0, 1, 0, 0],
[0, 0, 0, 1, 0, 0]
]
3. 암시적 그래프
그래프의 정점과 간선을 직접적으로 표현하지 않고,
필요한 상황에서 동적으로 그래프의 일부 또는 전체를 생성하거나 탐색하는 방식이다.
연결표시를 하지 않아도 주변이 연결되어있음을 암시적으로 알 수 있는 경우!
ex) 미로 찾기 문제
DFS(깊이우선탐색) vs BFS(너비우선탐색)

DFS(깊이우선탐색)
노드의 간선을 타고 깊이를 우선적으로 탐색함
스택 또는 재귀함수로 구현
스택: 쌓아놓은 더미. 마지막으로 넣은 걸 먼저 꺼낼 수 있음.
(
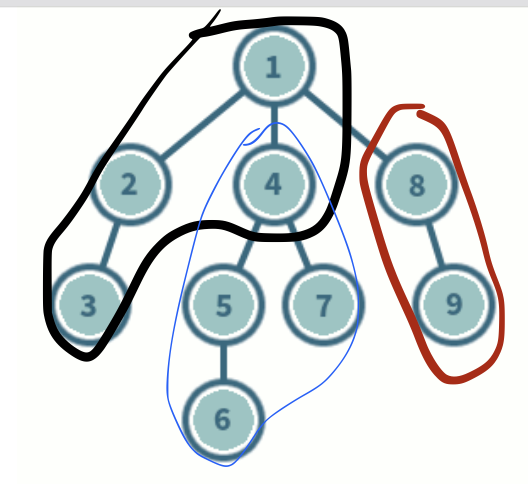
왼쪽 살펴서 있으면 깊이 끝까지 탐색 후 오른쪽.
오른쪽 노드가 다시 첫번째 노드가 되어서 왼쪽 깊이 탐색 후 오른쪽.
반복되어 재귀함수로 구현 가능. )
BFS(너비우선탐색)
전체 너비, 행순으로 탐색함
큐로 구현
큐: 버스 앞에 줄선 사람. 먼저 선 사람이 버스 탈 수 있음.
코드는 차후에 정리해보겟음..
컴백함. 정리해보겠음
--------------------
chatgpt한테 물어봄
DFS(깊이우선탐색) 알고리즘 코드구현
def dfs(graph, start, visited): #인자에 그래프, 시작노드, 방문한 노드 집합
visited.add(start) # 현재 노드를 방문 처리
print(start, end=' ')
# 현재 노드와 인접한 노드들을 순회
for adjacent_node in graph[start]:
if adjacent_node not in visited: #만약에 방문하지 않은 노드라면
dfs(graph, adjacent_node, visited) #그 노드를 시작노드로 해서 재귀함수 실행 -> 현재노드를 방문처리~ 반복
# 그래프를 인접 리스트로 표현한 예시
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
visited = set() # 방문한 노드를 저장하기 위한 집합
print("깊이 우선 탐색 결과:")
dfs(graph, 'A', visited)그래프의 모든 노드를 깊이를 우선하여 탐색하는 DFS는
재귀함수 또는 스택으로 구현될 수 있다.
여기서는 재귀함수로 구현됨
코드풀이~
시작노드를 방문처리하고
그 시작노드의 인접노드가 방문하지 않은 노드라면
해당 노드를 다시 시작노드로 설정해서 재귀함수~ (다시 그 시작노드로 방문처리하고 반복)
스택으로 구현한 코드
def dfs(graph, start):
visited = set() # 방문한 노드를 저장하기 위한 집합
stack = [start] # 탐색할 노드를 저장하기 위한 스택
while stack:
node = stack.pop() # 스택의 가장 위에 있는 노드를 가져옴
if node not in visited:
visited.add(node)
print(node, end=' ')
# 인접한 노드들 중에서 방문하지 않은 노드를 스택에 추가
for adjacent_node in graph[node]:
if adjacent_node not in visited:
stack.append(adjacent_node)
# 그래프를 인접 리스트로 표현한 예시
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
print("깊이 우선 탐색 결과:")
dfs(graph, 'A')
BFS 너비탐색 알고리즘 코드구현
from collections import deque
#먼저 collections 모듈에서 deque를 가져옵니다.
#deque는 양쪽 끝에서의 빠른 append와 popleft 연산을 지원하는 큐(queue) 자료구조입니다
#이 함수는 그래프와 시작노드를 인자로 받는다.
def bfs(graph, start):
visited = set() # 방문한 노드를 저장하기 위한 집합 초기셋팅
queue = deque([start]) # 탐색할 노드를 저장하기 위한 큐
visited.add(start) # 시작 노드를 방문 처리
#큐가 비어있지 않은 동안 반복한다
while queue:
node = queue.popleft() # 큐에서 가장 앞에 있는 노드를 가져옴. popleft를 해서큐에서 노드를 제거
print(node, end=' ')
# 인접한 노드들 중에서 방문하지 않은 노드를 큐에 추가하고 방문 처리
for adjacent_node in graph[node]: #현재 처리중인 node의 인접한 노드들을 순회
if adjacent_node not in visited:#방문했다는 집합에 해당노드가 없다면
queue.append(adjacent_node) #큐에다가 인접 노드 넣기
visited.add(adjacent_node) #방문했다고 방문집합에 추가하기
# 그래프를 인접 리스트로 표현한 예시
graph = {
'A': ['B', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F'],
'D': ['B'],
'E': ['B', 'F'],
'F': ['C', 'E']
}
print("너비 우선 탐색 결과:")
bfs(graph, 'A')
코드풀이는 다음과 같다~
선택한 시작 노드 주변을 확인.
(인접노드 확인).
확인할 애들을 큐에 저장
확인마친, 즉 방문한 애들은 방문집합에 저장.
큐가 텅빌때까지 반복
확인할 노드는 큐에서 꺼내서 씀. 맨 처음 넣은 앞에서부터 꺼낼거임
그래프의 현재 노드 주변에 있는 애들을 for문 반복문으로 다 확인해볼것임
방문집합에 해당 노드가 없다면 방문안한거니까
아까 꺼냈던 노드를 큐에다가 다시 추가
그리고 그 노드에 방문(그 노드를 탐색)한거니까 방문집합에 그 노드를 넣는다.
'코딩테스트 > 백준' 카테고리의 다른 글
| 백준 1920번 이진탐색으로 (0) | 2023.06.15 |
|---|---|
| 정렬 (0) | 2023.05.30 |
| for문과 while차이점 (0) | 2023.05.15 |
| 파이썬 = , == , elif (0) | 2023.05.15 |
| 재귀함수, Binary Tree 이진트리, 트리순회traversal,너비우선탐색BFS, 깊이우선탐색 DFS (2) | 2023.04.23 |